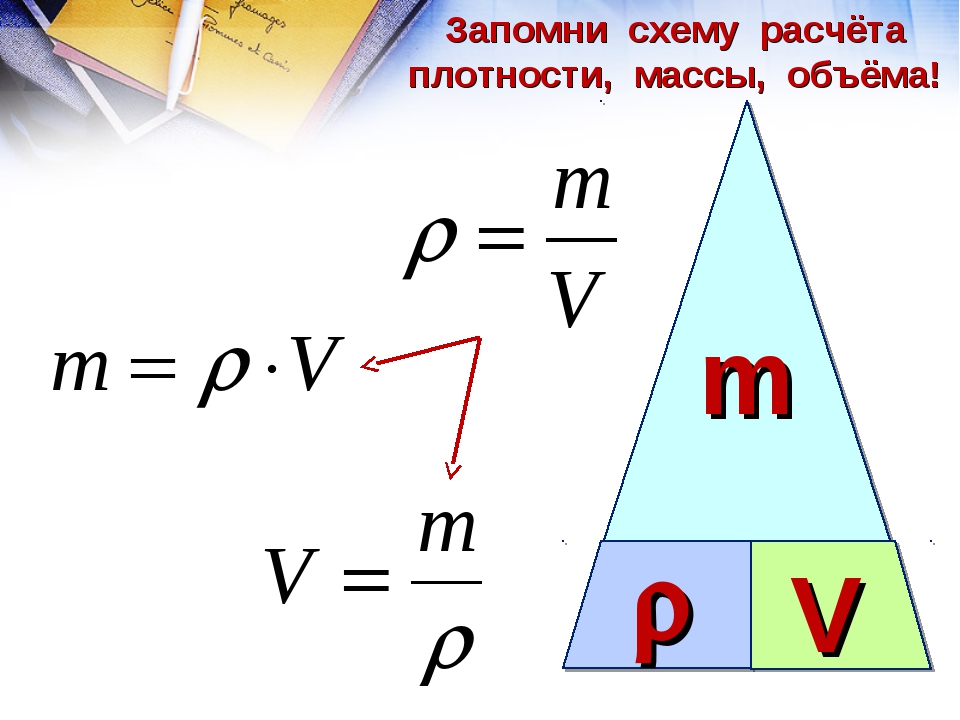
Формула расчета массы: Формула массы тела в физике
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми.
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
| Плотность материалов | |
| Наименование | Плотность ρ, кг/м3 |
| Черные металлы | |
| Сталь 10 ГОСТ 1050-88 | 7856 |
| Сталь 20 ГОСТ 1050-88 | 7859 |
| Сталь 40 ГОСТ 1050-88 | 7850 |
| Сталь 60 ГОСТ 1050-88 | 7800 |
| С235-С375 ГОСТ 27772-88 | 7850 |
| Ст3пс ГОСТ 380-2005 | |
| Чугун ковкий КЧ 70-2 ГОСТ 1215-79 | 7000 |
| Чугун высокопрочный ВЧ35 ГОСТ 7293-85 | 7200 |
| Чугун серый СЧ10 ГОСТ 1412-85 | 6800 |
| Чугун серый СЧ20 ГОСТ 1412-85 | 7100 |
| Чугун серый СЧ30 ГОСТ 1412-85 | 7300 |
| Алюминий и сплавы алюминиевые | |
| Силумин АК12ж ГОСТ 1583-93 | 2700 |
| Сплав АК12 ГОСТ 1583-93 | 2710 |
| Сплав АК5М ГОСТ 1583-93 | 2640 |
| Сплав АК7 ГОСТ 1583-93 | 2700 |
| Сплав АО9-1 ГОСТ 14113-78 | 2700 |
| Магний и сплавы магниевые | |
| Сплав ВМЛ9 | 1850 |
| Сплав ВМЛ5 | 1890 |
Сплав МЛ10. ..МЛ19 ГОСТ 2856-79 |
1810 |
| Баббиты оловянные и свинцовые | |
| Б83 ГОСТ 1320-74 | 7380 |
| Б87 ГОСТ 1320-74 | 7300 |
| БН ГОСТ 1320-74 | 9550 |
| Медь и медные сплавы | |
| Бронза оловянная БрО10C10 | 8800 |
| Бронза оловянная БрО19 | 8600 |
| Бронза оловянная БрОC10-10 | 9100 |
| Бронза оловянная БрОA10-1 | 8750 |
| Бронза БрА10Ж3Мч2 ГОСТ 493-79 | 8200 |
| Бронза БрА9Ж3Л ГОСТ 493-79 | 8200 |
| Бронза БрМц5 ГОСТ 18175-78 | 8600 |
| Латунь Л60 ГОСТ 15527-2004 | 8800 |
| Латунь ЛА ГОСТ 1020-97 | 8500 |
| Медь М0, М1, М2, М3 ГОСТ 859-2001 | 8940 |
| Медь МСр1 ГОСТ 16130-90 | 8900 |
| Титан и титановые сплавы | |
| ВТ1-0 ГОСТ 19807-91 | 4500 |
| ВТ14 ГОСТ 19807-91 | 4500 |
| ВТ20Л ГОСТ 19807-91 | 4470 |
| Фторопласты | |
| Ф-4 ГОСТ 10007-80 Е | 2100 |
| Фторопласт — 1 ГОСТ 13744-87 | 1400 |
| Фторопласт — 2 ГОСТ 13744-87 | 1700 |
| Фторопласт — 3 ГОСТ 13744-87 | 2710 |
| Фторопласт — 4Д ГОСТ 14906-77 | 2150 |
| Термопласты | |
| Дакрил-2М ТУ 2216-265-057 57 593-2000 | 1190 |
| Полиметилметакрилат ЛПТ ТУ 6-05-952-74 | 1180 |
| Полиметилметакрилат суспензионный ЛСОМ ОСТ 6-01-67-72 | 1190 |
| Винипласт УВ-10 ТУ 6-01-737-72 | 1450 |
| Поливинилхлоридный пластикат ГОСТ 5960-72 | 1400 |
| Полиамид ПА6 блочный Б ТУ 6-05-988-87 | 1150 |
| Полиамид ПА66 литьевой ОСТ 6-06-369-74 | 1140 |
| Капролон В ТУ 6-05-988 | 1150 |
| Капролон ТУ 6-06-309-70 | 1130 |
| Поликарбонат | 1200 |
| Полипропилен ГОСТ 26996-86 | 900 |
| Полиэтилен СД | 960 |
| Лавсан литьевой ТУ 6-05-830-76 | 1320 |
| Лавсан ЛС-1 ТУ 6-05-830-76 | 1530 |
| Стиролпласт АБС 0809Т ТУ 2214-019-002 03521-96 | 1050 |
| Полистирол блочный ГОСТ 20282-86 | 1050 |
| Сополимер стирола МСН ГОСТ 12271-76 | 1060 |
| Полистирол ударопрочный УПС-0505 ГОСТ 28250-89 | 1060 |
| Стеклопластик ВПС-8 | 1900 |
| Стеклотекстолит конструкционный КАСТ-В ГОСТ 10292-74 | 1850 |
| Винилискожа-НТ ГОСТ 10438-78 | 1440 |
| Резина 6Ж ТУ 38-005-1166-98 | 1050 |
| Резина ВР-10 ТР 18-962 | 1800 |
| Стекло листовое ГОСТ 111-2001 | 2500 |
| Стекло органическое техническое ТОСН ГОСТ 17622-72 | 1180 |
| Прочие металлы | |
| Вольфрам ВА ГОСТ 18903-73 | 19300 |
| Вольфрам ВТ-7 ГОСТ 18903-73 | 19300 |
| Золото Зл 99,9 ГОСТ 6835-2002 | 19300 |
| Индий ИНО ГОСТ 10297-94 | 7300 |
| Кадмий КдО ГОСТ 1467-93 | 8640 |
| Олово О1пч ГОСТ 860-75 | 7300 |
| Паладий Пд 99,8 ГОСТ 13462-79 | 12160 |
| Платина Пд 99,8 ГОСТ 13498-79 | 21450 |
| Свинец С0 ГОСТ 3778-98 | 11400 |
| Серебро 99,9 ГОСТ 6836-2002 | 11500 |
| Цинк Ц1 ГОСТ 3640-94 | 7130 |
| Прочие материалы | |
| Древесина, пробка | 480 |
| Древесина, лиственница | 660 |
| Древесина, липа | 530 |
| Древесина, ель | 450 |
| Древесина, сосна | 520 |
| Древесина, береза | 650 |
| Древесина, бук | 690 |
| Бумага | 700-1200 |
| Резина | 900-2000 |
| Кирпич | 1400-2100 |
| Фарфор | 2300 |
| Бетон | 2000-2200 |
| Цемент | 2800-3000 |
таблицы и рекомендации для расчета
Стальной шестигранник – разновидность сортового проката со сплошным сечением шестигранной формы.
Характеристики и области применения
Для изготовления шестигранников рядового назначения используют углеродистые стали обыкновенного качества и качественные конструкционные. Для производства продукции, предназначенной для использования при высоких нагрузках, в условиях пониженных температур, в агрессивных средах, – низколегированные и легированные.
Горячекатаный и калиброванный шестигранник применяют в:
- машиностроении;
- производстве крепежа;
- строительстве, архитектуре и дизайне;
- производстве инструмента;
- автомобилестроении;
- мебельном производстве.
Определение веса стального шестигранника по таблицам
Для проектирования конструкций и механизмов необходимо знать массу детали из шестигранника. Для этого необходимо массу 1 м умножить на требуемую длину.
Таблица веса 1 м стального шестигранника
|
Диаметр вписанного круга, d, мм |
Масса 1 м, кг |
Диаметр вписанного круга, d, мм |
Масса 1 м, кг |
Диаметр вписанного круга, d, мм |
Масса 1 м, кг |
Диаметр вписанного круга, d, мм |
Масса 1 м, кг |
|
10 |
0,68 |
19 |
2,45 |
29 |
5,27 |
43 |
12,71 |
|
11 |
0,82 |
20 |
2,72 |
30 |
6,12 |
46 |
14,53 |
|
12 |
0,98 |
21 |
3 |
32 |
6,96 |
47 |
14,95 |
|
13 |
1,15 |
22 |
3,29 |
34 |
7,86 |
48 |
15,66 |
|
14 |
1,33 |
24 |
3,92 |
36 |
8,81 |
50 |
16,98 |
|
15 |
1,53 |
25 |
4,25 |
38 |
9,82 |
52 |
18,4 |
|
16 |
1,74 |
26 |
4,59 |
40 |
10,86 |
55 |
20,58 |
|
17 |
1,96 |
27 |
4,96 |
41 |
11,54 |
57 |
22,35 |
|
18 |
2,2 |
28 |
5,33 |
42 |
11,99 |
60 |
24,5 |
Табличные данные являются справочной информацией, для их определения была использована средняя плотность стали – 7,85 кг/м3.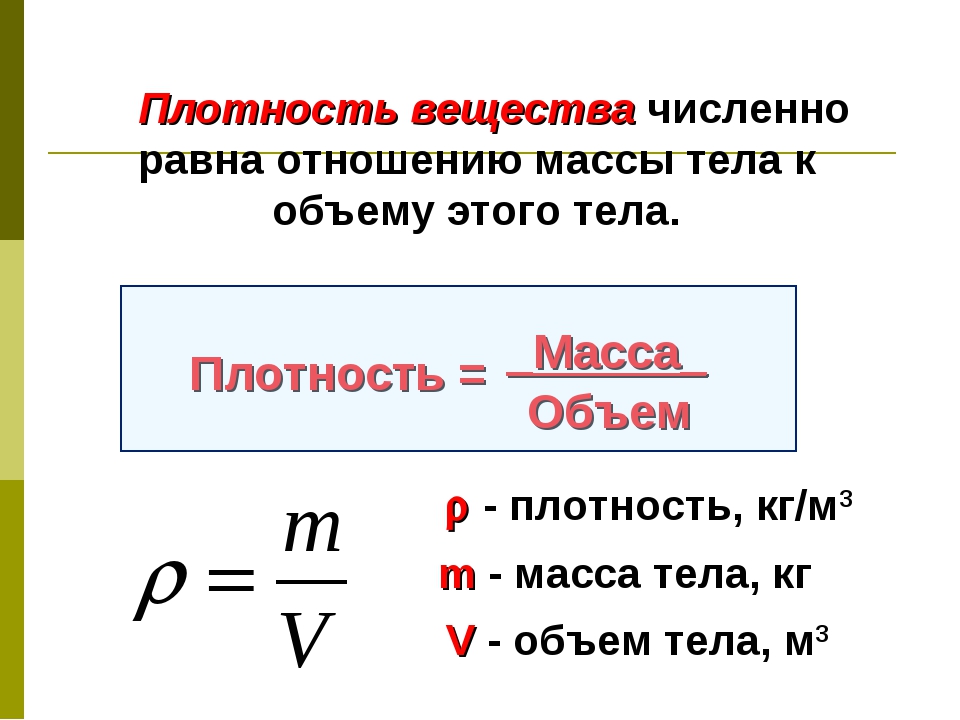
Расчет веса стального шестигранника по формуле
При отсутствии справочных таблиц массу проката с шестигранным сечением можно рассчитать с помощью формулы.
M = 0,87*d2*7,85/1000, где:
M – масса 1 м, кг;
d – диаметр вписанной окружности, мм (номер шестигранного проката).
Для быстрого расчета массы шестигранника удобны онлайн-калькуляторы, рассчитанные на изделия из сталей различных марок и цветные металлы и сплавы.
7.6. Формула расчета масс элементарных частиц
7.6. Формула расчета масс элементарных частиц.
Закон тяготения Ньютона
определяет силу, с которой взаимодействуют две массы на расстоянии от их центров ( на расстоянии сферических окрестностей их гравитационных радиусов) r.
Потенциал взаимодействия равен и по логике представляет энергию взаимодействия (дефект массы).
Таким образом, можно записать
Полевая гравитационная энергия вычисляется по формуле
Закон электромагнитного взаимодействия двух элементарных зарядов выражается в виде
.Потенциал взаимодействия определяется по формуле
и представляет дефект энергии взаимодействия и может быть выражен через энергию поляОткуда полевая энергия взаимодействия масс
с зарядами е,е будет выражаться формулойПолученные соотношения по новому определяют физическую характеристику потенциала при взаимодействии частиц. Энергия взаимодействия частиц есть дефект масс взаимодействующих частиц. Разность потенциалов определяет изменение дефекта массы при изменение расстояния между взаимодействующими частицами. Полевая энергия учитывается в формулах величинами
.Определим при каких условиях полевая энергия дает эквивалентность электромагнитного и гравитационного дефекта при взаимодействии.
Если
то получаем зависимость где -есть соответственно расстояния электромагнитного и гравитационного взаимодействия. Преобразования даютЕсли
, то получимТаким образом, эквивалентность гравитационного и электромагнитного полей определено фундаментальной гравитационной массой
Если
имеем электромагнитную массу частицыB исследованиях начала координат и гравитационного радиуса поля тяготения Шварцшильда было получено соотношение, которое в комплексном пространстве отделяет пространство одной частицы от пространства другой. Другими словами при переходе через поверхность гравитационного радиуса частицы попадаем в пространство другой частицы.
Рассмотрим взаимодействие двух частиц с позиций этого соотношения. Проведем последовательно преобразования
, , ,
Для соблюдения предыдущего равенства необходимо, чтобы гравитационный радиус был равен удвоенной комптоновской длине волны частицы
.
Комптоновская длина волны протона равна
Определим массу протона
Таким образом, протон есть результат взаимодействия двух фундаментальных масс
на расстоянии комптоновской длины волны протона. Это взаимодействие дает массу протона.
Комптоновская длина волны электрона равна
Классический радиус электрона
.Рассчитаем массы электрона
Электромагнитная масса электрона равна
Таким образом, элементарные частицы протон и электрон есть результат гравитационного взаимодействия двух фундаментальных масс
на расстоянии равном комптоновской длине волны этих частиц . Элементарные частицы есть результат дефекта масс при взаимодействии. Полевая энергия взаимодействия для протона равнаКривизна пространства, которую задают фундаментальные массы, определяют огромную полевую энергию их взаимодействия между собой.
9раз превышают его собственную энергетическую массу.
Преобразование интервала поля тяготения ШВАРЦШИЛЬДА по законам пространственной комплексной алгебры показывает, что гравитационная фундаментальная масса
создает в пространстве комплексную особенность в виде сферической -окрестности радиуса, равному фундаментальной длине .В микромире нет евклидового пространства. ВСЕ ПРОСТРАНСТВО ПСЕВДОЕВКЛИДОВО, поэтому не должно существовать различия в описании электромагнитных и гравитационных взаимодействий. РАСЧЕТ ПОКАЗАЛ, ЧТО НА ФУНДАМЕНТАЛЬНОМ РАССТОЯНИИ ДЛЯ ФУНДАМЕНТАЛЬНЫХ МАСС ГРАВИТАЦИОННОЕ ПОЛЕ АДЕКВАТНО ЭЛЕКТРОМАГНИТНОМУ.
ВЗАИМОДЕЙСТВИЕ ФУНДАМЕНТАЛЬНЫХ МАСС НА РАССТОЯНИЯХ РАВНЫХ КОМПТОНОВСИМ ДЛИНАМ ВОЛН МИКРОЧАСТИЦ ДАЮТ МАССУ ЭТИХ ЧАСТИЦ.
[Следующий параграф]
Мини оглавление:
[0], [1.1.1, 1.1.2, 1.1.3,
1.
1.4, 1.1.5, 1.1.6,
1.1.7, 1.1.8, 1.2,
1.2.1, 1.2.2, 1.2.2.a,
1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1,
1.3.2, 1.3.3, 1.3.4,
1.3.5, 1.3.6, 1.4.1,
1.4.2, 1.5, 1.6, 1.7.1, 1.7.2,
1.7.3.1, 1.7.3.2, 1.7.3.3,
1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3,
3.4.1, 3.4.2, 3.4.3,
3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3,
5.4, 5.4.Т1, 5.4.Т2,
5.4.Т3, 5.5.1, 5.5.2,
5.5.3, 5.5.4],[6.1.1,
6.1.2, 6.2.1, 6.2.2,
6.2.3, 6.2.4, 6.2.5,
6.3, 6.4.1, 6.4.2,
6.5.1, 6.5.2],[7.1,
7.2, 7.3, 7.4,
7.5, 7.6, 7.7.1,
7.7.2, 7.8.1, 7.8.2,
7.8.3, 7.9],[8.1,
8.2.1, 8.2.2, 8.3,
8.4, 8.5, 8.6,
8.6.T1, 8.7, 8.8.1,
8.8.2, 8.8.3, 8.9.1,
8.9.2, 8.9.3, 8.10,
8.10.T2, 8.10.T3],[9.1,
9.2, 9.3, Рис.88,
89, 90, 91,
92, 93, 94,
95, 96, 97,
98, 99, 100],[10.1,
10.2, 10.3, 10.4,
10.
5, 10.6, 10.7,
10.8, 10.9, 10.10,
10.11, 10.12, 10.13,
10.14, 10.15.1, 10.15.2,
10.16.1, 10.16.2, 10.17,
10.18],[11]
Размещенный материал является электронной версией книги: © В.И.Елисеев, «Введение в методы теории функций пространственного комплексного переменного», изданной Центром научно-технического творчества молодежи Алгоритм. — М.:, НИАТ. — 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.
E-mail: [email protected]
Расчет веса стальной трубы по формуле
Довольно часто возникает потребность расчёта веса стального трубопроката, который собственно заключатся в расчёте веса одного погонного метра трубы.
В данной статье мы поможем сделать эти вычисления и узнать, вес трубы в зависимости от её характеристик.
Для расчёта веса трубы можно использовать несколько вариантов, одним из них является специальная таблица веса стальных труб, другим ГОСТ веса труб, а так же расчёт по специальным формулам.
Сегодня мы рассмотрим последний вариант, а именно расчёт веса трубы по формулам.
Данные формулы практически не отличаются по своим результатам, и вполне подходят для расчёта веса стального трубопроката.
Сразу стоит сказать, что имеющиеся две формулы расчёта массы трубы, не ограничиваются, какими то видами стальных труб, это могут быть и газовые и электросварочные трубы, расчёт их веса неизменен и результат будет верным (в пределах этих формул).
Зная формулы и необходимости расчёта веса стального металлопроката, в зависимости от его характеристик вы можете использовать одну из предложенных формул.
Теперь давайте перейдём непосредственно к формулам.
Первая формула по расчёту веса стального металлопроката:
Мп = ((Ду – Тс)/40,5)*Тс.
Где,
Ду – собственно диаметр стальной трубы, который измеряется в миллиметрах;
Тс – это толщина стенки стальной трубы, мера измерения миллиметры;
Мп – вес погонного метра трубы.
Теперь перейдём ко второй формуле расчёта веса труб из стали:
Вот собственно вторая наша формула: Мп = (Ду – Тс)*Тс*0,0246615,
Где,
Ду – диаметр стальной трубы, измеряемый в миллиметрах;
Тс – толщина стенки трубы из стали, единицы измерения миллиметры;
Мп – итоговый результат, как и в прошлой формуле, представляет собой вес одного погонного метра стальной трубы.
Как видите в данных формулах нет ничего сложного, для их использования и вычисления веса труб не требуется особых знаний и умений, достаточно знать формулы и иметь под ругой калькулятор.
Читайте так же:
Как правильно выбрать и купить арматурные изделия
Стальные отводы, общая информация
Технология изготовления арматуры
| 3. Решение задач | |
| 1. Как будем выставлять оценку за работу на уроке по принципу сложения или вычитания? | По принципу сложения. |
| 2. Таблица 1 (Приложение №1). На складе имеются грузы: мел, пробка, береза, лед, сталь. Каждый груз упакован в контейнеры по 2 м3. для перевозки этих грузов были вызваны пять автомобилей. Ваша задача распределить грузы по автомобилям. | Найти массу грузов. |
| — Что нужно сделать, чтобы распределить грузы по автомобилям? | |
| — Как найти массу вещества, если известна его плотность и объём? | кг/м3 |
| — В каких единицах измерена плотность вещества? | В килограммах |
| — В каких единицах будет вычислена масса? | В тоннах и килограммах |
| — В каких единицах выражена грузоподъемность автомобилей? | В тоннах, а для москвича в килограммах |
| — В каких единицах нужно получить массу грузов? Решите
данную задачу и распределите грузы по
автомобилям. Учитель проверяет правильность выполненного задания у первого решившего ученика, и назначает его своим ассистентом. В карточках (Приложение № 3) учеников делаются записи количества набранных баллов. |
Ученики решают задачи и распределяют грузы. |
| 3. Таблица 2 (Приложение № 2).
Имеются пять различных жидкостей, которые имеют
одинаковую массу. Эти жидкости нужно разлить по
пяти различным сосудам. — Что нужно сделать, чтобы разлить жидкости по сосудам? |
Найти объём жидкостей. |
| — Как найти объем, если известна масса вещества и его плотность? | |
| — В каких единицах получится вычисленный объём? | в м3. |
| — В каких единицах дан объём сосудов? | В литрах и миллилитрах |
| — В каких единицах нужно получить объём жидкостей? | В литрах и миллилитрах |
Решите данную задачу и распределите жидкость
по сосудам. Учитель проверяет правильность выполненного задания у первого решившего ученика, и назначает его своим ассистентом. В карточках учеников делаются записи количества набранных баллов. |
Ученики решают задачу. |
| 4. Рефлексия. | |
| — Какие физические понятия Вы использовали для
выполнения заданий? Сравните количество баллов, которые вы выставили сами себе, с количеством баллов, которые вам выставили проверяющие. Какой вы можете для себя сделать вывод? Готовы ли вы к контрольной работе? |
Масса, плотность, объем. |
Основные Химические формулы для решения задач.
| № | Количественные характеристики вещества | Обозначение | Единицы измерения | Формула для расчета |
|---|---|---|---|---|
| 1 | Плотность вещества | ρ | кг/м³ | ρ = m / V(Массу делим на объем вещества) |
| 2 | Относительная атомная масса элемента | Аr | — | Ar = ma / u см.  в периодической система химических элементов |
| 3 | Атомная единица массы | u а.е.м. | кг | u = 1/12 * ma (12C) const = 1.66*10-27 |
| 4 | Масса атома (абсолютная) | ma | кг | ma = Ar * u |
| 5 | Относительная молекулярная (формульная) масса вещества | Mr | — | Mr (AxBy)=m(AB) / u Mr(AxBy)=x*Ar(A) + y*Ar(B) |
| 6 | Масса молекулы (формульной единицы) | m M | кг | mM = Mr*u |
| 7 | Количество вещества | n | моль | n=m/M n=N/NA n=V/VM |
| 8 | Молярная масса (масса 1 моль вещества) | M | г/моль | M=m/n M=Mr M=Ar (для простых веществ) |
| 9 | Масса вещества | m | г (кг) | m=M*n m=ρ*V |
| 10 | Число структурных единиц | N | атомов, молекул, ионов, частиц, формульных единиц (Ф. Е.) | N=NA*n |
| 11 | Молярный объем — число 1 моль ГАЗООБРАЗНОГО вещества в нормальных условиях (н.у.) | VM | л/моль | const=22,4 |
| 12 | Объем газа при н.у. | V | л | V=VM*n V=m/ρ |
| 13 | Постоянная Авогадро | NA | частиц/моль | const=6,02*1023 |
| 14 | Массовая доля вещества (омега) | ωЭ/В | % | ωЭ/В = (Ar(э) * k) / Mr(В) |
| Формула | Название кислоты | Формула кислотного остатка | Название кислотного остатка |
|---|---|---|---|
| HF | Фтороводород, плавиковая | F— | Фторид |
| HCl | Хлороводород, соляная | Cl— | Хлорид |
| HBr | Бромоводород | Br— | Бромид |
| HI | Йодоводород | I— | Йодид |
| h3S | Сероводород | S2- | Сульфид |
| HCN | Циановодородная | CN— | Цианид |
| HNO2 | Азотистая | NO2— | Нитрит |
| HNO3 | Азотная | NO3— | Нитрат |
| h4PO4 | Ортофосфорная | PO43- | Фосфат |
| h4AsO4 | Мышьяковая | AsO43- | Арсенат |
| h3SO3 | Сернистая | SO32- | Сульфит |
| h3SO4 | Серная | SO42- | Сульфат |
| h3CO3 | Угольная | CO32- | Карбонат |
| h3SiO3 | Кремниевая | SiO32- | Силикат |
| h3CrO4 | Хромовая | CrO42- | Хромат |
| h3Cr2O7 | Дихромовая | Cr2O72- | Дихромат |
| HMnO4 | Марганцовая | MnO4— | Перманганат |
| HClO | Хлорноватистая | ClO— | Гипохлорит |
| HClO2 | Хлористая | ClO2— | Хлорит |
| HClO3 | Хлорноватая | ClO3— | Хлорат |
| HClO4 | Хлорная | ClO4— | Перхлорат |
| HCOOH | Метановая, муравьиная | HCOO— | Формиат |
| Ch4COOH | Этановая, уксусная | Ch4COO— | Ацетат |
| h4C2O4 | Этандиовая, щавелевая | C2O42- | Оксалат |
Нажмите на картинку для увеличения
Что такое формула массы?
Масса — это свойство физических объектов и мера устойчивости этого тела к ускорению.
Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.
В отличие от реляционных свойств, таких как положение, скорость или потенциальная энергия, которые всегда должны определяться по отношению к другому объекту или контрольной точке, масса является внутренним свойством , которое объект имеет независимо от его отношения к другим вещам.Массу объекта можно рассчитать несколькими способами:
- масса = плотность × объем (m = ρV) . Плотность — это мера массы на единицу объема, поэтому массу объекта можно определить, умножив плотность на объем.
- масса = сила ÷ ускорение (м = F / a) . Согласно второму закону Ньютона (F = ma) ускорение объекта прямо пропорционально приложенной к нему силе. Следовательно, величина ускорения, сопровождающая приложение постоянной силы, обратно пропорциональна массе.
- масса = вес ÷ ускорение свободного падения (м = Вт / г). Вес — это произведение ускорения массы в гравитационном поле. В зависимости от силы ускорения свободного падения вес будет разным.
Вес — это произведение ускорения массы в гравитационном поле. В зависимости от силы ускорения свободного падения вес будет разным.Все три формулы являются способом определения массы объекта. Поскольку масса является фундаментальным свойством, она не определяется в других единицах, как джоуль (Дж) ньютона (Н). Есть и другие способы вычисления массы объекта, но эти три формулы являются наиболее распространенными.
м = ρV
м = Вт / г
м = F / a
Единицы массы
Единица измерения массы, принятая в системе СИ, килограмм (кг). Килограмм — единственная основная единица СИ, имеющая в названии префикс (килограмм). Первоначально один килограмм определялся как масса одного кубического децилитра (дл) воды при температуре плавления. В 1889 году килограмм был переопределен как масса International Kilogram Prototype (IPK), физического артефакта, который должен был быть универсальной эталонной массой для килограмма.
Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятый ИПК представляет собой цилиндр высотой 39 мм из специального платинового сплава.
«Слова тоже имеют подлинную сущность — массу, вес и удельный вес». — Тим О’Брайен
По состоянию на 2018 год килограмм — единственная единица СИ, в которой физический объект является опорным значением. Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка.В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за переопределение килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года.
Способы расчета массы
на основе плотности и объема
Плотность объекта, иногда обозначаемая греческой буквой «ρ», является мерой массы на единицу объема. По сути, плотность говорит вам, насколько плотно упакована масса объекта.
Чем плотнее объект, тем больше у него массы на единицу объема.
Например, вода имеет плотность 977 кг / м 3 при стандартной температуре и давлении. То есть один кубометр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Допустим, у нас есть образец воды размером 0,7 м 3 . Какова масса этого образца?
Решение для массы дает:
m = ρV
m = (0,7 м 3 ) (977 кг / м 3 ) = 683 кг
0.5 кубометров воды при стандартной температуре и давлении имели бы массу 683 кг.
Некоторые объекты невероятно плотные. Например, нейтронная звезда имеет среднюю плотность 1,1 x 10 18 кг / м 3 . Одна чайная ложка нейтронной звезды на Земле будет весить около 100 миллионов тонн.
«Масса становится неподвижной; он не может маневрировать и, следовательно, не может одерживать победы, он может сокрушить только своим весом ».
— Hans Von SeecktОт силы и ускорения
Свойство массы также понимается как мера сопротивления физического объекта ускорению под действием внешней силы.Это понятие массы иногда называют инерционной массой . Инерция — это тенденция движущегося тела продолжать движение в постоянном состоянии, поэтому инерционная масса — это мера того, сколько инерции имеет тело и насколько сложно изменить его состояние движения. Связь между массой, силой и ускорением выражается вторым законом движения Ньютона F = ma. Это математическое соотношение говорит нам, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее.Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Например, предположим, что мы прикладываем силу 748 Н к металлическому кубу и измеряем его ускорение как 21 м / с 2 . Какая масса у металлического куба? Мы можем вычислить массу, разделив величину силы на величину ускорения:
м = F / a
м = (748 Н) / (21 м / с 2 ) ≈ 35,62 кг
Итак, мы знаем, что металлический куб должен иметь массу 35.
62 кг.
From Вес
Строго говоря, вес и масса — разные вещи. В английском языке два слова «вес» и «масса» являются синонимами, но в физических науках они имеют разные значения. Масса — неизменное свойство, которое не меняется от места к месту. Вес — это мера силы гравитационного поля, действующего на массивное тело. Поскольку напряженность гравитационного поля может различаться, то есть Луна имеет более слабую напряженность гравитационного поля, чем Земля, вес объекта может различаться в разных средах.
Связь между массой и весом определяется выражением W = mg, где g — мера ускорения свободного падения. Точное значение g различается в зависимости от местоположения. На Земле g имеет значение приблизительно 9,81 м / с 2 , а на Луне g составляет около 1,6 м / с 2 . Выражение W = мг дает вес в ньютонах, в то время как повседневное понимание веса дано в фунтах (фунтах), коэффициент преобразования из ньютонов в фунты составляет около 1 Н = 0,22 фунта.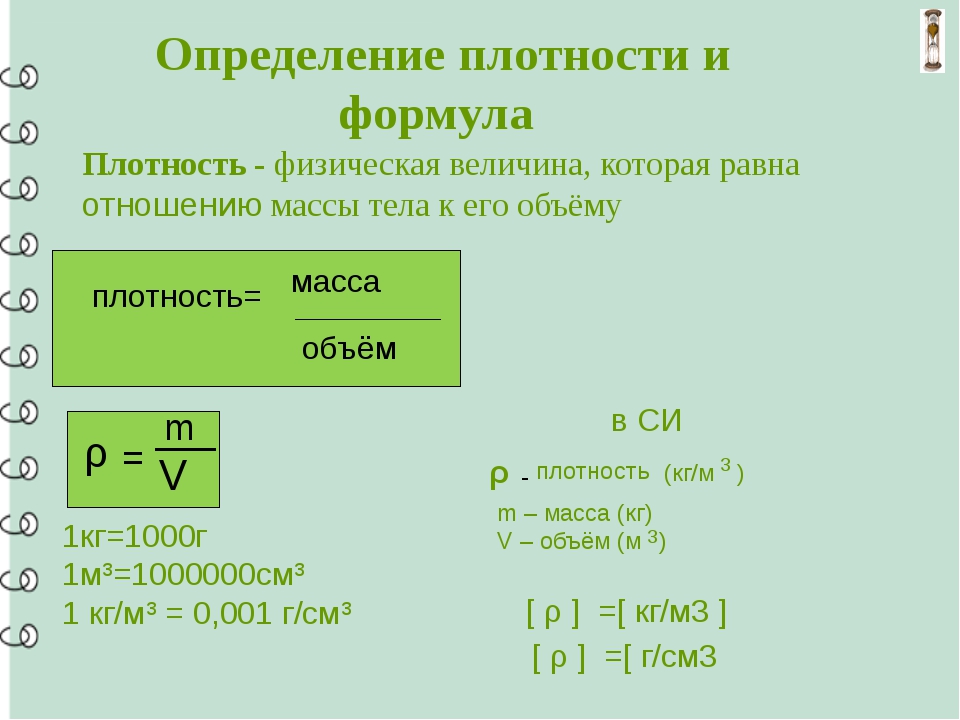
Например, на поверхности Земли где g = 9.81 м / с 2 , объект весом 50 кг будет иметь вес в фунтах:
W = (50 кг) (9,81 м / с 2 ) = 490,5N
Преобразование ньютонов в фунты дает:
490,5 Н (0,22 фунта / 1 Н) ≈ 108 фунтов
И наоборот, на Луне, где g имеет значение 1,6 м / с 2 , объект весом 50 кг будет весить:
W = 50 (кг) ( 1,6 м / с 2 ) (0,22 фунта / 1 Н) ≈ 18 фунтов
Тот же объект весом 50 кг весит 108 фунтов на Земле и 18 фунтов на Луне.
Точно так же, если мы знаем вес объекта, мы можем работать в обратном направлении, чтобы вычислить его массу. Скажем, объект весит 160 фунтов Земли. мы можем рассчитать массу объекта как:
180 фунтов (1N / 0,22 фунта) = 818,18N
818,18N = м (9,81 м / с 2 )
м = 818,18N / (9,81 м / с 2 ) ≈ 83,4 кг
Таким образом, тело на Земле весом 180 фунтов имеет массу около 84,3 кг.
Эквивалентность массы и энергии
В течение очень долгого времени ученые считали, что массу объекта можно считать полностью независимой от других его свойств.Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E = mc 2 , где c — скорость света в вакууме.
E = mc 2 говорит нам, что полная энергия неподвижного тела прямо пропорциональна его массе с коэффициентом c 2 . Поскольку c = 3 000 000 м / с, c 2 является чрезвычайно большим фактором.Следовательно, даже крошечный кусочек массы содержит огромное количество внутренней энергии. Чтобы рассмотреть вопрос в перспективе, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам в тротиловом эквиваленте — силе атомной бомбы в Хиросиме.
«Любой дурак может знать. Дело в том, чтобы понять ». — Альберт Эйнштейн
В определенных физических процессах, таких как ядерное деление или движение тела в сильном гравитационном поле, материя преобразуется в энергию и выделяется в виде большого количества света и тепла.В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, выделяющейся во время таких реакций.
Скажем, 30 кг урана (Ur) загружают в ядерный реактор. Во время деления примерно 0,1% этой массы полностью превращается в энергию. Сколько энергии получается?
0,1% от 30 кг составляет 0,3 кг. Подставив это в уравнение Эйнштейна, мы получим:
E = (0,3 кг) (3,000,000) 2 = (0,3) (8,98755179 × 10 16 ) = 2,69626554 × 10 16 J
Полное преобразование всего 0 .3 кг (0,6 фунта) вещества превращаются в энергию, выделяя 2,69626554 × 10 16 Дж энергии. Это примерно столько же, сколько взорвано более 6 миллионов тонн тротила (12 миллиардов фунтов), чего достаточно, чтобы полностью сравнять с землей даже самые большие города.
Мы также можем работать в обратном направлении от некоторого количества энергии, чтобы определить количество преобразованной массы. Скажем, некоторая реакция деления высвобождает 1,6178 × 10 16 джоулей энергии. Сколько массы было преобразовано в энергию во время этого процесса? Используя нашу удобную формулу эквивалентности массы и энергии, мы можем определить:
1.6178 × 10 16 J = м (8,98755179 × 10 16 )
(1,6178 × 10 16 ) / 8,98755179 × 10 16 ) = м
м ≈ 0,18 кг
Таким образом, примерно 0,18 кг масса была преобразована в энергию.
Почему объекты имеют массу?
Только недавно ученые начали открывать ответ на вопрос, почему частицы вообще имеют массу. В 1960-х годах несколько ученых заметили некоторые проблемы со своими уравнениями, описывающими поведение элементарных частиц.В частности, их уравнения предсказывали, что определенные частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы.
Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
Ученые предположили, что масса бозона может быть образована взаимодействием между этими бозонами и всепроникающим полем, называемым полем Хиггса (в честь одного из его теоретиков Питера Хиггса). Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют некоторую энергию.Поле Хиггса преобразует эту энергию в массу-энергию, которая проявляется как масса свойства, которую мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса приведет к созданию новой частицы, крошечного бозона, получившего название бозона Хиггса. Ускоритель элементарных частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглерт были удостоены Нобелевской премии по физике за их теоретические работы по частице.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.
Расчет масс по формуле
Расчет масс по формуле
Так как молекула — поцарапайте ее, мы снова идем, называя все молекулами! С формула состоит из атомов, мы можем вычислить формулу массы, просто сложив все атомы, которые в нем. Это приложение закона сохранения массы. Считать увеличьте количество атомов каждого типа в формуле и сложите общую массу. У нас есть в этих примерах это разбито в виде таблицы, и вы, вероятно, захотите использовать в чем-то похожий метод.
| Что из следующего является правильным расчетом формулы массы? |
Если формула содержит многоатомные ионы, количество атомов в скобках умножается на любой нижний индекс сразу за скобками, как показано в этом пример.
Вот еще один пример многоатомного иона.
| Что из следующего является правильным расчетом формулы массы? |
Иногда, когда образуются ионные кристаллы, вода становится частью кристаллической структуры.
Этот
известна как гидратная вода, а кристаллы называются «гидратами» или
«гидратированные соли». Формулы для гидратов всегда включают разделитель точек, за которым следует
по количеству присоединенных молекул воды, например по формулам типа CuSO 4 . 5H 2 O.
Есть несколько способов составить такие формулы. Один из методов — очистить воду
гидратации как имеющей собственную массу, и добавьте ее к другим массам, как показано на этом рисунке.
пример.
| Что из следующего является правильным расчетом формулы массы? |
Все вышеупомянутые примеры ионных формул, но применяется точно такой же принцип к истинным молекулярным формулам, таким как глюкоза.
| С точностью до двух знаков после запятой, какова формула массы CH 3 CH 2 OH (спирт этиловый)? |
В каждом из приведенных выше примеров атомные массы округлены до второго десятичного знака.
Некоторые атомные массы элементов известны гораздо точнее, чем это
— и немного меньше! Наиболее точно известна атомная масса фтора, равная 18.9984032.
Атомная масса свинца, равная 207,2, является одной из менее точных, потому что содержание его изотопов сильно варьируется в зависимости от
места на земле. Содержание изотопа серы также очень непостоянно, поэтому оно имеет ошибку.
около 0,01% по атомной массе в различных местах на Земле. Этого недостаточно, чтобы повлиять
большинство химических расчетов. Однако вы всегда должны сообщать об ответах, используя значимые
цифры правильно.
| Что из следующего может уточнить атомную массу атома? Отметить все что применимо. |
Расчет масс по формуле сначала может показаться немного сложным и таким же сложным для понимания, как и финансовые инструменты, такие как калькуляторы аннуитета.
Это станет намного проще, если приложить немного усилий и терпения. Приведенные выше примеры и вопросы — отличный способ попрактиковаться в вычислении масс по формуле.
Авторские права 1998–2008 Дэвид Дайс
Расчет относительных масс по формуле — Расчет массы по формуле и молей — Редакция GCSE Chemistry (Single Science) — Другое
Относительная масса по формуле
Относительные атомные массы можно использовать для нахождения относительной массы по формуле соединения.
Чтобы найти относительную формульную массу (M r ) соединения, вы складываете значения относительной атомной массы (значения A 
0.0.0.1:0.1.0.$0.$2.$2.$3″> r ) для всех атомов в его формуле.
Вот два примера:
- Вопрос
Найдите M r окиси углерода, CO.
- Показать ответ
Углерод A r равен 12 и A r кислорода равно
0.0.0.1:0.1.0.$0.$2.$4.3.$0.$7″> 16 .M r окиси углерода составляет 12 + 16 = 28 .
- Вопрос
Найдите M r оксида натрия, Na 2 O.
- Показать ответ
A
$0.$2.$5.3.$0.$1″> r натрия составляет 23 и A r кислорода 16 .M r оксида натрия составляет (23 × 2) + 16 = 62 .
Относительная формульная масса вещества, выраженная в граммах, называется на один моль этого вещества.Таким образом, один моль оксида углерода имеет массу 28 г, а один моль оксида натрия имеет массу 62 г.
В таблице приведены еще несколько примеров расчета относительной формулы массы с использованием значений относительной атомной массы, приведенных в нижней части страницы.
Массово-молярные вычисления Учебное пособие по химии
Пожалуйста, не блокируйте рекламу на этом сайте.
Без рекламы = для нас нет денег = для вас нет бесплатных вещей!
Расчет массы чистого вещества (m = нМ)
1 моль чистого вещества определяется как имеющий массу в граммах, равную его относительной молекулярной массе.
Эта величина известна как молярная масса (символ M).
Итак, масса 1 моля чистого вещества = относительная молекулярная масса в граммах.
А, масса 1 моля чистого вещества = молярная масса чистого вещества (г моль -1 )
Или, масса 1 моля = M (г моль -1 )
В таблице ниже указана масса 1 моля ряда обычных чистых веществ:
| название | молекулярная формула | относительная молекулярная масса | молярная масса (г моль -1 ) | масса 1 моля (г) | ||||
|---|---|---|---|---|---|---|---|---|
| газообразный гелий | He | 4. 003 | 4,003 г моль -1 | 4,003 г | ||||
| газообразный кислород | O 2 | 2 × 16,00 = 32,00 | 32,00 г моль -1 | 328 328 | углекислый газCO 2 | 12,01 + (2 × 16,00) = 44,01 | 44,01 г моль -1 | 44,01 г |
| жидкая вода | H 2 O | (2 × 1,008) + 16.00 = 18,016 | 18,016 г моль -1 | 18,016 г |
Из таблицы мы видим, что 1 моль воды имеет массу 18,016 грамма, что не очень много (примерно по массе воды в паре маленьких кубиков льда, которые вы бы сделали в своей семейной морозильной камере).
Но что, если бы у вас было 10 молей воды? Какой будет масса 10 молей воды?
Если 1 моль воды имеет массу 18,016 г, то 10 моль воды должны иметь массу в десять раз больше:
масса 10 моль воды = 10 × масса 1 моля воды
масса 10 моль воды = 10 × 18.
016 = 180,16 г (примерно масса воды, которую можно налить в небольшой стакан)
Итак, если бы у нас было только ½ моля воды, какая масса воды была бы у нас?
Если 1 моль воды имеет массу 18,016 г, то ½ моля воды должно иметь ½ массы:
масса ½ моля воды = ½ × масса 1 моля воды
масса ½ моля воды = ½ × 18,016 = 9,008 г
В обоих приведенных выше примерах мы можем вычислить массу воды в граммах, умножив количество молей воды на массу 1 моля воды в граммах:
масса воды = моль воды × масса 1 моля воды
, поскольку масса 1 моля воды в граммах известна как его молярная масса, мы можем записать:
масса воды = моль воды × молярная масса воды
В таблице ниже сравнивается масса различных количеств воды в молях:
| масса воды (г) | = | моль воды (моль) | × | масса 1 моля воды (молярная масса воды) (г-моль -1 ) | |
|---|---|---|---|---|---|
| 0 | = | 0. 00 | × | 18,016 | |
| 9,008 | = | 0,50 | × | 18,016 | |
| 18,016 | = | 1,00 9023 9023 9023 9023 9023 9023 9023 9023 9023 9023 9023 9023 | 1,50 | × | 18,016 |
| 180,16 | = | 10,00 | × | 18,016 | |
| 270.24 | = | 15,00 | × | 18,016 |
Из данных в таблице мы можем обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна количеству молей вещества, умноженных на массу 1 моля вещества:
масса = моль × масса 1 моля
, а поскольку масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль)
масса (г) = моль × молярная масса (г моль -1 )
м = n × M
где
m = масса чистого вещества в граммах
n = количество чистого вещества в молях
M = молярная масса чистого вещества в граммах на моль
Мы также можем нанести данные из таблицы выше на график, как показано ниже:
| масса (г) | 051015300250200150100500 |
| моль (моль) |
На приведенном выше графике показана прямая линия, проходящая через начало координат (0,0), поэтому уравнение для прямой выглядит следующим образом:
y = уклон × x
где:
y — масса воды (г)
x — моль воды (моль)
наклон (уклон) линии = вертикальный подъем ÷ горизонтальный ход
Мы можем определить наклон прямой, используя 2 точки на прямой, например (0,0) и (15.
0, 270,24):
наклон = (270,24 г — 0 г) ÷ (15 моль — 0 моль) = 18,016 г моль -1
Поскольку 18,016 г моль -1 — это молярная масса воды, мы можем сказать:
наклон = молярная масса воды (г · моль -1 )
Следовательно, уравнение для этой линии:
масса (H 2 O) = молярная масса (H 2 O) × моль (H 2 O)
Всего:
масса (г) = молярная масса (г-моль -1 ) × моль (моль)
Исходя из данных в таблице и ее графического представления, мы можем обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна молям вещества, умноженным на массу 1 моля вещества:
масса = моль × масса 1 моля
, а поскольку масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль)
масса (г) = моль × молярная масса (г моль -1 )
м = n × M
Выполните следующие действия, чтобы рассчитать массу чистого вещества с учетом количества вещества в молях:
- Шаг 1. Извлеките данные из вопроса:
- Шаг 2. Проверьте единицы на соответствие и при необходимости преобразуйте:
- Шаг 3. Напишите математическое уравнение (математическую формулу):
- Шаг 4. Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).
Извлеките данные из вопроса:масса = m =? (единицы граммы)
родинок = n = запишите, что вам сказали в вопросе
молярная масса = M = запишите, что вам говорят в вопросе (единицы измерения: г-моль -1 )
(вам может потребоваться вычислить это, используя молекулярную формулу чистого вещества и Периодическую таблицу)
Количество вещества должно быть в молях (моль)!
Если количество указано в миллимолях (ммоль), разделите его на 1000, чтобы получить количество в молях (моль).
Если количество указано в микромолях (мкмоль), разделите его на 1 000 000, чтобы получить количество в молях (моль).
Если количество указано в километрах (кмоль), умножьте его на 1000, чтобы получить количество в молях (моль).
масса = моль × молярная масса
или
м = n × M
Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).Расчет молей чистого вещества (n = m / M)
В ходе обсуждения выше мы обнаружили, что можем рассчитать массу чистого вещества, используя моль и молярную массу вещества:
масса (г) = моль (моль) × молярная масса (г-моль -1 )
Как бы мы вычислили количество молей чистого вещества, если бы мы знали массу вещества?
(a) Мы могли бы использовать некоторую алгебру: разделите обе части уравнения на молярную массу:
| масса | = | моль × | |||||||||||||||||||||||||||||
| молярная масса | молярная масса моль = масса ÷ молярная масса п = м ÷ М или (b) Мы могли бы использовать некоторую логику:
При осмотре единиц мы видим, что деление молярной массы на массу даст нам количество в единицах «моль -1 » молярная масса / масса = Если мы перевернем это вверх дном (математически, возьмем обратную величину), мы получим количество в единицах «моль», которое нам и нужно: масса / молярная масса = т. моль = масса ÷ молярная масса п = м ÷ М Выполните следующие действия, чтобы рассчитать количество чистого вещества в молях с учетом массы вещества:
масса = m = запишите, что вам сказали в вопросе моль = n =? (ед. моль) молярная масса = M = запишите, что вам говорят в вопросе (единицы измерения: г-моль -1 ) (вам может потребоваться вычислить это, используя молекулярную формулу чистого вещества и Периодическую таблицу) Масса должна быть в граммах! Если масса указана в миллиграммах (мг), разделите ее на 1000, чтобы получить массу в граммах (г). Если масса дана в микрограммах (мкг), разделите ее на 1000000, чтобы получить массу в граммах (г). Если масса указана в килограммах (кг), умножьте ее на 1000, чтобы получить массу в граммах (г). моль = масса ÷ молярная масса или п = м ÷ М Расчет молярной массы чистого вещества (M = m / n) Что, если бы вы знали количество чистого вещества в молях и его массу? Напомним, что масса = моль × молярная масса или m = n × M (a) Мы могли бы использовать некоторую алгебру: разделите обе части уравнения на моли:
|
5 г газообразного кислорода.
Для химикатов с малой массой
вида, выбранный изотоп часто является наиболее
обильный изотоп вида; однако это часто не
случай для более крупных массовых видов из-за
потребность в более сложном алгоритме, чтобы сделать такой
определение.
Калькулятор распределения изотопов и плоттер масс-спектрометрии.
Однако обратите внимание, что синтаксически допустимая формула («CH6»)
не обязательно семантически действителен; эта программа делает
никаких усилий по определению семантической достоверности.В течение
фаза синтаксического анализа, вычисления выполняются (т. е. генерируются).
Удобно, что этапы разбора и генерации
могут быть тесно связаны.
моль — это единица измерения количества вещества. Один моль «чего-то» содержит 6,022 x 1023 объекта. Например, в одном моль химического соединения 6.022 х 1023 молекул.
Этот же метод расчета также можно использовать для определения объема при каком-либо другом наборе условий. Чтобы преобразовать массовый расход в объем, используйте следующее уравнение:
Это также можно было бы назвать ACFM (Фактические кубические футы в минуту).
